高效的检索和访问海量信息是处理它们的重要前提。查找应运而生。
下面将介绍几种经典的数据类型与查找算法,包括:
- 二分查找
- 二叉查找树
- 平衡二叉树(红黑树)
- 散列表
二分查找
二分查找基于有序数组,核心思想是通过不断判断目标值所在区间而确定目标值位置的方法,核心在于不断修改中间值。其迭代的实现如下:
1
2
3
4
5
6
7
8
9
10
11
| function binarySearch(arr, key){
var lo = 0,
hi = arr.length-1
while(lo <= hi){
var mid = Math.floor(lo + (hi-lo)/2)
if (arr[mid] === key) return mid
else if (arr[mid] > key) hi = mid - 1
else if (arr[mid] < key) lo = mid + 1
}
return -1
}
|
其递归的实现如下:
1
2
3
4
5
6
7
8
9
10
| function binarySearch(arr, key, lo, hi){
if (hi < lo) return -1
var lo = lo || 0,
hi = hi || arr.length- 1 ,
mid = Math.floor(lo + (hi-lo)/2)
if (arr[mid] === key) return mid
else if (arr[mid] > key) return binarySearch(arr, key, lo, mid - 1)
else if (arr[mid] < key) return binarySearch(arr, key, mid + 1, hi)
return -1
}
|
在数组有序的情况下,二分查找可以很快的实现查找,平均情况下查找次数需要lgN次。平均插入成本为N,最坏插入成本为2N。
二叉查找树

二叉查找树(binary search tree)由结点组成,结点包含了链接,链接可以为空或指向其子节点。子节点分为左子节点和右子节点。
在二叉查找树中,每个结点还包含一个键和一个值,键之间有序,以支持高效的查找。
二叉查找树具有以下重要的性质:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
而且,二叉树与快速排序具有一定的相似性。二叉树的根节点可以看做是快速排序的第一个切分元素(左小又大),且对于子树完全适用,这和快速排序中对子数组的递归排序完全适用。
二叉查找树的实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
| class BST {
constructor() {
this.root = null
}
Node(key) {
let left = null,
right = null
return {
key,
left,
right
}
}
insert(key) {
if (this.root === null) {
this.root = this.Node(key)
} else {
this.insertNode(this.root, newNode)
}
}
insertNode(node, newNode) {
if (node.key > newNode.key) {
if (node.left === null) {
node.left = newNode
} else {
this.insertNode(node.left, newNode)
}
} else {
if (node.key < newNode.key) {
if (node.right === null) {
node.right = newNode
} else {
this.insertNode(node.right, newNode)
}
}
}
}
min() {
return this.minNode(this.root)
}
minNode(node) {
if (node) {
while (node && node.left !== null) {
node = node.left
}
return node.key
} else {
return null
}
}
max() {
return this.maxNode(this.root)
}
maxNode(node) {
if (node) {
while (node && node.right !== null) {
node = node.right
}
return node.key
} else {
return null
}
}
search(key) {
return this.searchNode(this.root, key)
}
searchNode(node, key) {
if (node === null) {
return false
}
if (key > node.key) {
return this.searchNode(node.right, key)
} else if (key < node.key) {
return this.searchNode(node.left, key)
} else {
return true
}
}
inOrderTraverse(callback) {
return this.inOrderTraverseNode(this.root, callback)
}
inOrderTraverseNode(node, callback) {
if (node !== null) {
this.inOrderTraverseNode(node.left, callback)
callback(node.key)
this.inOrderTraverseNode(node.right, callback)
}
}
preOrderTraverse(callback) {
return this.preOrderTraverseNode(this.root, callback)
}
preOrderTraverseNode(node, callback) {
if (node !== null) {
callback(node.key)
this.preOrderTraverseNode(node.left, callback)
this.preOrderTraverseNode(node.right, callback)
}
}
postOrderTraverse(callback) {
return this.postOrderTraverseNode(this.root, callback)
}
postOrderTraverseNode(node, callback) {
if (node !== null) {
this.postOrderTraverseNode(node.left, callback)
this.postOrderTraverseNode(node.right, callback)
callback(node.key)
}
}
invert(node = this.root) {
if (node !== null) {
this.invert(node.left)
this.invert(node.right)
this.exchange(node)
}
}
exchange(node) {
let temp = node.left
node.left = node.right
node.right = temp
}
}
|
二叉查找树存在的问题
使用二叉查找树算法的运行时间取决于树的形状,而树的形状取决于键被插入的先后顺序,最坏情况下,搜索路径上有N个结点。

正是由于二叉查找树的这种不平衡性质导致查找与插入的时间没有保证,因此一种平衡的二叉树即平衡二叉树应运而生。
平衡二叉树
我们希望完美的二叉树是平衡的,即根节点到每一个叶节点的距离相等,也可以看做是一颗含有N个结点的树中,树高为~lgN。
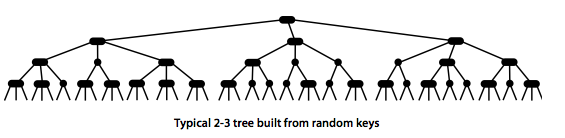
为了保证树的平衡性,需要一些灵活性。因此引入3-结点以区分二叉查找树中的2-结点
定义:一颗平衡二叉树由以下结点组成
- 2-结点:含有一个键(及其对应的值),两个链接,左链接指向的键都小于该结点,右链接指向的键都大于该结点
- 3-结点:含有两个键(及其对应的值),三个链接,左链接指向的键都小于该结点,右链接指向的键都大于该结点,中链接指向的键都位于该结点的两个键之间
一颗完美平衡的平衡二叉树中,所有空链接到根节点的距离是相同的。而平衡二叉树的关键在于所有局部变换都不会影响整棵树的平衡性和有序性
下面给出平衡二叉树插入结点的过程,注意观察在插入过程中二叉树的调整,至平衡的过程(图为红黑树,但只要将红链接连接的两个节点看成一个3-节点,即为平衡二叉树)
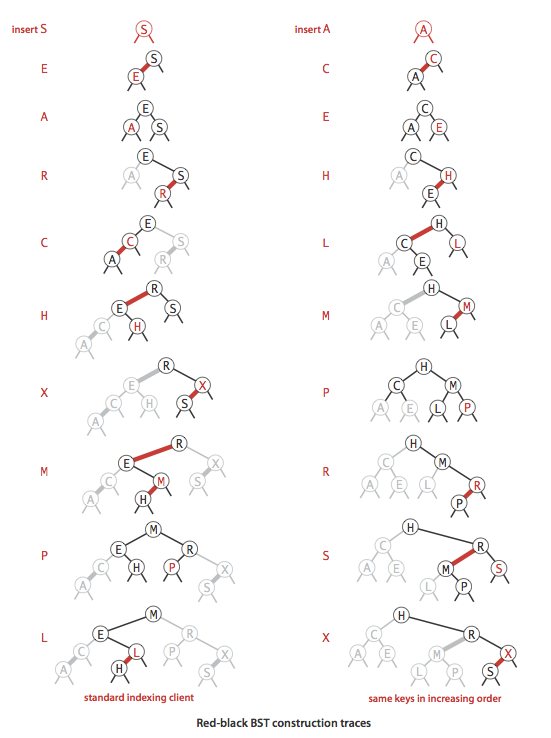
红黑树
虽然可以用直白的方式表示出平衡二叉树,单由于在插入结点时要判断的情况过多,难以实现。而在引入了红黑键的情况下,则可以以一种统一的方式实现二叉查找树到平衡二叉树的变换,即红黑树。
红黑树的基本思想是用标准的二叉查找树和额外的键颜色信息来表示平衡二叉树,红链接将2个2-结点相连,构成一个3-结点,黑链接为普通链接。
红黑树具有以下性质:
- 红链接均为左链接
- 没有任何一个结点同时与两条红链接相连
- 该树是完美黑色平衡的
可以看到红黑树的结点信息中多出了结点键颜色变量:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class redBlackTree {
constructor() {
this.root = null
}
Node(key, color) {
let left = null,
right = null
return {
key,
color,
left,
right
}
}
}
|
散列表
尽管平衡二叉树的查找插入效率很高,但是实现略显复杂。而散列表可以使用简单的方法处理复杂键的值。散列算法的核心是散列函数,其作用为给定一个键值,返回值在表中的位置
散列表是在时间和空间上做出权衡的典型例子。当没有内存限制时
下面给出散列表的基本实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class hashTable {
constructor() {
this.table = []
}
hashCode(key) {
let hash = 5381
for (let i in key) {
hash = hash*33 + key.charCodeAt(i)
}
return hash % 1013
}
put(key, val) {
let pos = this.hashCode(key)
console.log(`${pos}-${key}`)
this.table[pos] = val
}
get(key) {
return this.table[this.hashCode(key)]
}
remove(key) {
let pos = this.hashCode(key)
this.table[pos] = undefined
}
}
|
该散列表根据输入的字符串键进行散列运算,获取键,然后置入散列表中。但是这种方法不是没有问题的,当给定不同输入,经过散列函数处理得到相同的键时,便产生了碰撞冲突
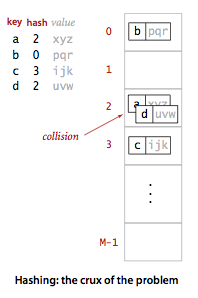
要解决碰撞冲突有两种办法,即拉链法(分离链接法)与线性探测法
拉链法(分离链接法)
拉链法即为散列表的每一个位置创建一个链表,并将重复的元素储存在里面,但它在创建hashTable之外还要额外的储存空间

且相应的put,get等方法都要做出改动,下面仅给出put方法的实现,其他方法类似,都要引入链表。
1
2
3
4
5
6
7
8
9
10
|
function put(key, value){
let pos = hashCode(key)
if(table[pos] === undefined){
table[pos] = new LinkedList()
}
table[pos].append(new ValuePair(key, value))
}
|
线性探测法
线性探测法的思想即:当向表中某一个位置加入一个新元素时,如果索引位于index的键已经被占用了,就尝试index+1,如果依然占用,就尝试index+2,以此类推
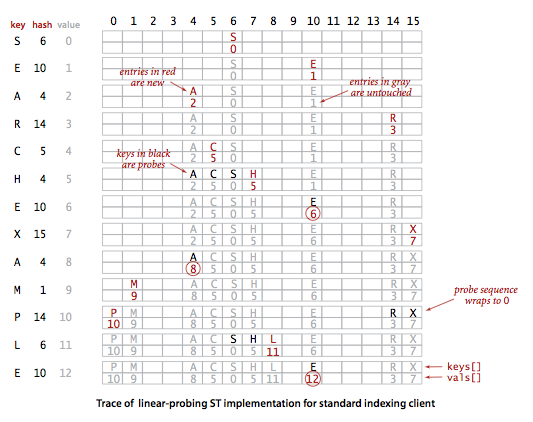
下面给出线性探测法put方法的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| function put(key, value) {
let pos = hashCode(key)
if (table[pos] === undefined) {
table[pos] = new ValuePair(key, value)
} else {
let index = pos
while (++index) {
if (table[pos] === undefined) {
table[pos] = new ValuePair(key, value)
break
}
}
}
}
|
各数据结构性能及优缺点比较
综上,可以评价出各种查找方法的优缺点。从以下性能表中可以看出,对于典型的应用程序,应该选择平衡二叉树或散列表方法。
由于散列表的实现较简单且查找时间最优,大部分情况下我们选择散列表进行查找操作。
| 数据结构 |
最坏查找 |
最坏插入 |
平均查找 |
平均插入 |
內存使用 |
| 无序链表 |
N |
N |
N/2 |
N |
48N |
| 有序数组(二分) |
lgN |
N |
lgN |
N/2 |
16N |
| 二叉查找树 |
N |
N |
1.39lgN |
1.39lgN |
64N |
| 红黑树 |
2lgN |
2lgN |
lgN |
lgN |
64N |
| 拉链法 |
<lgN |
<lgN |
N/2M |
N/M |
48N+32M* |
| 线性探测法 |
clgN |
clgN |
<1.5 |
<2.5 |
32N-128N |
| 数据结构 |
优点 |
缺点 |
| 有序数组(二分查找) |
最优的查找效率和空间需求,能够进行有序性相关操作 |
插入操作很慢 |
| 二叉搜索树 |
实现简单,能进行有序性相关操作 |
没有性能上界的保证,链接需要额外空间 |
| 平衡二叉树 |
最优的查找和插入效率,能够进行有序性相关操作 |
链接需要额外空间 |
| 散列表 |
能够快速查找和插入常见的数据类型 |
需要计算每种数据类型的散列,无法进行有序性相关操作,链接和空节点需要额外空间 |






